Descriptive analyses
Bas Hofstra
Last compiled on May, 2025
This is the code with which we render our descriptive analyses
1 Initatiating R environment
Start out with a custom function to load a set of required packages.
# packages and read data
rm(list = ls())
# (c) Jochem Tolsma
fpackage.check <- function(packages) {
lapply(packages, FUN = function(x) {
if (!require(x, character.only = TRUE)) {
install.packages(x, dependencies = TRUE, repos = "http://cran.us.r-project.org")
library(x, character.only = TRUE)
}
})
}
packages = c("haven", "coda", "matrixStats", "parallel", "MASS", "doParallel", "dplyr", "cowplot", "tidyverse",
"naniar", "dotwhisker", "gt", "reshape2", "VGAM", "expss", "Hmisc", "poweRlaw", "fitdistrplus", "grid",
"ggplotify", "smplot2")
fpackage.check(packages)#> [[1]]
#> NULL
#>
#> [[2]]
#> NULL
#>
#> [[3]]
#> NULL
#>
#> [[4]]
#> NULL
#>
#> [[5]]
#> NULL
#>
#> [[6]]
#> NULL
#>
#> [[7]]
#> NULL
#>
#> [[8]]
#> NULL
#>
#> [[9]]
#> NULL
#>
#> [[10]]
#> NULL
#>
#> [[11]]
#> NULL
#>
#> [[12]]
#> NULL
#>
#> [[13]]
#> NULL
#>
#> [[14]]
#> NULL
#>
#> [[15]]
#> NULL
#>
#> [[16]]
#> NULL
#>
#> [[17]]
#> NULL
#>
#> [[18]]
#> NULL
#>
#> [[19]]
#> NULL
#>
#> [[20]]
#> NULL
#>
#> [[21]]
#> NULLrm(packages)
load("data/dutch_netsize_analyses_revision_2.rda")2 Descriptives independent variables
The code below generates the descriptive values which are used for Tables 1 and 2.
# descriptive table not automated: TABLE 1
table(df$work)#>
#> 0 1
#> 583 666psych::describe(df$work)#> vars n mean sd median trimmed mad min max range skew kurtosis se
#> X1 1 1249 0.53 0.5 1 0.54 0 0 1 1 -0.13 -1.98 0.01psych::describe(df$hhsize)#> vars n mean sd median trimmed mad min max range skew kurtosis se
#> X1 1 1249 2.13 1.12 2 1.98 1.48 1 8 7 1.34 2.26 0.03table(df$agecat)#>
#> 4 1 2 3
#> 299 208 230 512# 1 Maj 2 west 3 nonwest
table(df$income)#>
#> 2 1 3
#> 440 627 182# 1 < modal 2 > modal 3 unknown
psych::describe(df$worthhouse)#> vars n mean sd median trimmed mad min max range skew kurtosis se
#> X1 1 1249 2.67 0.89 2.54 2.58 0.73 0.95 9.96 9.01 1.75 7.12 0.03table(df$woman)#>
#> 0 1
#> 609 640psych::describe(df$woman)#> vars n mean sd median trimmed mad min max range skew kurtosis se
#> X1 1 1249 0.51 0.5 1 0.52 0 0 1 1 -0.05 -2 0.01table(df$opl2)#>
#> 0 1
#> 783 466summary(df$opl2)#> Min. 1st Qu. Median Mean 3rd Qu. Max.
#> 0.0000 0.0000 0.0000 0.3731 1.0000 1.0000# 1 prim/sec 2 lower tert 3 higher tert
# psych::describe(df$neighdens)
# this is for the correlation table df$educ3 <- df$opl df$educ3 <-
# as.numeric(as.character(df$educ3))
table(df$migr3)#>
#> 1 2 3
#> 1131 62 56# cor(as.matrix(df[df$income!=3,c('income','worthhouse')]))
# rcorr(as.matrix(df[,c('work', 'hhsize', 'leeftijd10', 'woman', 'educ3', 'neighdens', 'worthhouse'
# )]), type = 'pearson')# table 2
summary(df$perwomen)#> Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
#> 0.0000 0.4800 0.6571 0.6108 0.7861 1.0000 11summary(df[df$woman == 1, c("perwomen")])#> Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
#> 0.0000 0.5498 0.7148 0.6564 0.8158 1.0000 4summary(df[df$woman == 0, c("perwomen")])#> Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
#> 0.0000 0.4223 0.5994 0.5626 0.7346 1.0000 7summary(df$permen)#> Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
#> 0.0000 0.2139 0.3429 0.3892 0.5200 1.0000 11summary(df[df$woman == 1, c("permen")])#> Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
#> 0.0000 0.1842 0.2852 0.3436 0.4502 1.0000 4summary(df[df$woman == 0, c("permen")])#> Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
#> 0.0000 0.2654 0.4006 0.4374 0.5777 1.0000 7summary(df$samegender)#> Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
#> 0.0000 0.3503 0.5709 0.5499 0.7590 1.0000 11summary(df[df$woman == 1, c("samegender")])#> Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
#> 0.0000 0.5498 0.7148 0.6564 0.8158 1.0000 4summary(df[df$woman == 0, c("samegender")])#> Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
#> 0.0000 0.2654 0.4006 0.4374 0.5777 1.0000 7summary(df$pereduchigh)#> Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
#> 0.000 0.400 0.750 0.652 1.000 1.000 640summary(df[df$opl2 == 1, c("pereduchigh")])#> Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
#> 0.0000 0.6667 1.0000 0.8085 1.0000 1.0000 191summary(df[df$opl2 == 0, c("pereduchigh")])#> Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
#> 0.0000 0.1952 0.5000 0.5231 1.0000 1.0000 449summary(df$pereduclow)#> Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
#> 0.000 0.000 0.250 0.348 0.600 1.000 640summary(df[df$opl2 == 1, c("pereduclow")])#> Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
#> 0.0000 0.0000 0.0000 0.1915 0.3333 1.0000 191summary(df[df$opl2 == 0, c("pereduclow")])#> Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
#> 0.0000 0.0000 0.5000 0.4769 0.8048 1.0000 449summary(df$sameeduc)#> Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
#> 0.0000 0.3333 0.6667 0.6266 1.0000 1.0000 640summary(df[df$opl2 == 1, c("sameeduc")])#> Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
#> 0.0000 0.6667 1.0000 0.8085 1.0000 1.0000 191summary(df[df$opl2 == 0, c("sameeduc")])#> Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
#> 0.0000 0.0000 0.5000 0.4769 0.8048 1.0000 449summary(df$netsover6)#> Min. 1st Qu. Median Mean 3rd Qu. Max.
#> 98.3 289.6 487.6 568.0 718.3 3590.93 Comparing naive estimations
The code below generates Figure 1 from the paper and runs a number of correlations found on page X.
# comps <- gather(df[, c('nsize_naive', 'nsize_b1b2', 'nsize_b3', 'nsize_n1', 'nsize_n2',
# 'nsize_n3', 'nsize_n123')]) comparisons <- ggplot(comps[comps$value < 2000, ], aes(x=value, color
# = key)) + geom_density(size = 0.5) + theme_minimal() + labs(x = 'Network size estimate', y =
# 'Density') + scale_color_manual(name = 'Estimation scenario', breaks = c('nsize_naive',
# 'nsize_b1b2', 'nsize_b3', 'nsize_n1', 'nsize_n2', 'nsize_n3', 'nsize_n123'), labels = c('Naive
# estimator: all X's', 'Battery 1: Tert. educ., elec vehicle, etc.', 'Battery 2: all names', 'Names
# 1: Sophie, Anna, Thomas, Willem', 'Names 2: Julia, Elisabeth, Max, Ali', 'Names 3: Sanne,
# Cornelia, Kevin, Mohammed', 'Names1+2+3'), values = c('#000000', '#E69F00', '#56B4E9', '#009E73',
# '#0072B2', '#D55E00', '#CC79A7', 'darkgrey')) # save ggsave('output/comparisons.pdf', plot =
# comparisons, device = 'pdf', scale = 1, width = 10, height = 5.5, units = c('in'), dpi =
# 'retina') # # correlation battery 1 and 2 # cor(df$nsize_b1, df$nsize_b2) # # # correlation
# battery 1 and all # cor(df$nsize_b1, df$nsize_naive) # correlation battery 1+2 and all
# cor(df$nsize_b1b2, df$nsize_naive) # correlation battery 3 (names) and all cor(df$nsize_b3,
# df$nsize_naive) # correlation names 1 and all cor(df$nsize_n1, df$nsize_naive) # correlation
# names 2 and all cor(df$nsize_n2, df$nsize_naive) # correlation names 3 and all cor(df$nsize_n3,
# df$nsize_naive) # correlation names 123 and all cor(df$nsize_n123, df$nsize_naive) # sample 5
# columns of scenarios and correlate with naive estimand set.seed(1987) sample(13:183, 5) #
# correlation scenario 85 and naive cor(df$nsize_naive, df[, 85]) # correlation scenario 36 and
# naive cor(df$nsize_naive, df[, 36]) # correlation scenario 150 and naive cor(df$nsize_naive, df[,
# 150]) # correlation scenario 14 and naive cor(df$nsize_naive, df[, 14]) # correlation scenario
# 125 and naive cor(df$nsize_naive, df[, 125]) comparisons4 Comparing Bayesian estimations
The code below generates Figure 2 from the paper associated with the text on page X.
# netsizes <- read.table(file = 'data/dutch_netsize_desc.txt') # VIZ of netsize netsize_l <-
# gather(netsizes) dens1 <- ggplot(netsize_l[netsize_l$value < 2000,], aes(x=value, color = key)) +
# geom_density(alpha = .2, size = 0.1) + theme_minimal() + theme(legend.position = 'none') + labs(x
# = 'Network size estimate', y = 'Density') +
# geom_vline(xintercept=as.numeric(psych::describe(netsize_l[, 2])[3]), color = 'darkgrey',
# linetype = 2) + geom_vline(xintercept=as.numeric(psych::describe(netsize_l[, 2])[5]), color =
# 'darkgrey', linetype = 2) + annotate('text', x = 490, y = 0.0004, color = 'darkgrey', angle = 90,
# label = paste0('Mean = ', round(as.numeric(psych::describe(netsize_l[, 2])[3]), digits = 0))) +
# annotate('text', x = 340, y = 0.0004, color = 'darkgrey', angle = 90, label = paste0('Median = ',
# round(as.numeric(psych::describe(netsize_l[, 2])[5]), digits = 0))) + ggtitle('B) Distribution of
# network sizes, all scenarios') # Get lower triangle of the correlation matrix
# get_lower_tri<-function(cormat){ cormat[upper.tri(cormat)] <- NA return(cormat) } mat <-
# cor(netsizes) lower_tri <- get_lower_tri(mat) melted_cormat <- reshape2::melt(lower_tri) #
# data.table also has melt funciton that won't work on matrices melted_cormat$Var2 <-
# as.character(melted_cormat$Var2) melted_cormat$Var1 <- as.character(melted_cormat$Var1)
# melted_cormat <- melted_cormat[!melted_cormat$Var2 == melted_cormat$Var1,] melted_cormat <-
# melted_cormat[!is.na(melted_cormat$value), ] # Viz of correlations between netsize estimates
# dens2 <- ggplot(melted_cormat, aes(x=value)) + geom_density(size = 0.3) + xlim(0.915, 1) +
# theme_minimal() + labs(x='Pearson correlation', y = 'Density') + geom_vline(xintercept = .95,
# color = 'darkgrey', linetype = 2) + ggtitle('A) Distributions of correlations between network
# size scenarios') + geom_segment(x = 0.95, y = 125, xend = .99, yend = 125, linetype = 2, color =
# 'darkgrey', arrow = arrow(length = unit(0.25, 'cm'))) + annotate('text', x = .97, y = 135, color
# = 'darkgrey', angle = 0, label = paste0(round(nrow(melted_cormat[melted_cormat$value > .95,
# ])/nrow(melted_cormat)*100, digits = 1),'% of correlations are > .95')) # lay 'm out on the grid
# denses <- plot_grid(dens2, dens1, nrow = 1) # save ggsave('output/densities.pdf', plot = denses,
# device = 'pdf', scale = 1, width = 12, height = 4, units = c('in'), dpi = 'retina') # denses5 Figure 1
The code below generates Figure 1 from the paper associated with the text on page X.
netsize_l <- data.frame(df[, c("netsover6")])
names(netsize_l) <- c("value")
round(summary(df$netsover6)[3], digits = 0)#> Median
#> 488round(summary(df$netsover6)[4], digits = 0)#> Mean
#> 568IQR(df$netsover6)#> [1] 428.6466dens1 <- ggplot(netsize_l, aes(x = value)) + geom_density(alpha = 0.2, size = 0.5) + theme_minimal() +
theme(legend.position = "none") + labs(x = "Network size estimate", y = "Density") + scale_color_manual(values = c("#56B4E9")) +
geom_vline(xintercept = 488, color = "darkgrey", linetype = 2) + geom_vline(xintercept = 568, color = "darkgrey",
linetype = 2) + annotate("text", x = 630, y = 4e-04, color = "black", angle = 90, label = "Mean = 568") +
annotate("text", x = 360, y = 4e-04, color = "black", angle = 90, label = "Median = 488") + xlim(c(0,
2500))
ggsave("output/densities1_revision.pdf", plot = dens1, device = "pdf", scale = 1, width = 5, height = 4,
units = c("in"), dpi = "retina")
ggsave("output/densities1_revision.jpeg", plot = dens1, device = "jpeg", scale = 1, width = 5, height = 4,
units = c("in"), dpi = "retina")
cor(df[, c("netsover1", "netsover2", "netsover4", "netsover5", "netsover6")])#> netsover1 netsover2 netsover4 netsover5 netsover6
#> netsover1 1.0000000 0.9999047 0.9425976 0.9990875 0.8936700
#> netsover2 0.9999047 1.0000000 0.9428511 0.9990386 0.8939040
#> netsover4 0.9425976 0.9428511 1.0000000 0.9400682 0.9585224
#> netsover5 0.9990875 0.9990386 0.9400682 1.0000000 0.8913483
#> netsover6 0.8936700 0.8939040 0.9585224 0.8913483 1.0000000# # VIZ of netsize scenarios netsize_l <- gather(df[, c('netsover1', 'netsover2', 'netsover4',
# 'netsover5', 'netsover6')]) round(summary(df$netsover6)[3], digits = 0)
# round(summary(df$netsover6)[4], digits = 0) dens2 <- ggplot(netsize_l, aes(x=value, color = key))
# + geom_density(alpha = .2, size = 0.5) + theme_minimal() + theme(legend.position = 'none') +
# labs(x = 'Network size estimate', y = 'Density') + scale_color_manual(values = c('grey', 'grey',
# 'grey', 'grey', '#56B4E9')) + geom_vline(xintercept=488, color = 'darkgrey', linetype = 2) +
# geom_vline(xintercept=568, color = 'darkgrey', linetype = 2) + annotate('text', x = 560, y =
# 0.0008, color = 'black', angle = 90, label = 'Mean = 568') + annotate('text', x = 400, y =
# 0.0008, color = 'black', angle = 90, label = 'Median = 488') + xlim(c(0, 2500)) # save
# ggsave('output/densities2_revision.pdf', plot = dens1, device = 'pdf', scale = 1, width = 5,
# height = 4, units = c('in'), dpi = 'retina') dens26 Distributional fit
We now fit a “complementary cumulative degree distribution” and check how it fits.
#df$netsize <- round(rowSums(df[,c(14:185)]) / length(14:185), 0)
df <- df[!df$netsover6 > 2500, ]
degrees <- round(df$netsover6, 0)
degr_pl <- displ$new(degrees) # create a discrete powerlaw distribution object
# with estimating lower threshold:
degr_ln_xmin <- dislnorm$new(degrees)
est = estimate_xmin(degr_ln_xmin)
degr_ln_xmin$setXmin(est)
# without lower threshold:
degr_ln_noxmin <-fitdist(degrees, "lnorm")
# Goodness of fit for lognorm, no xmin:
gof_degr_ln_noxmin <- gofstat(degr_ln_noxmin, fitnames = "Log-normal", discrete = TRUE)
gof_degr_ln_noxmin#> Chi-squared statistic: 397.1896
#> Degree of freedom of the Chi-squared distribution: 26
#> Chi-squared p-value: 4.716077e-68
#> Chi-squared table:
#> obscounts theocounts
#> <= 114 42.00000 19.04267
#> <= 155 42.00000 38.18254
#> <= 189 43.00000 47.59966
#> <= 220 41.00000 53.06053
#> <= 235 45.00000 28.07115
#> <= 277 42.00000 83.65007
#> <= 286 47.00000 18.48203
#> <= 329 42.00000 88.69643
#> <= 337 42.00000 16.36047
#> <= 380 42.00000 85.81643
#> <= 389 42.00000 17.37445
#> <= 427 41.00000 70.57309
#> <= 438 42.00000 19.51967
#> <= 448 42.00000 17.37170
#> <= 490 44.00000 68.97153
#> <= 505 42.00000 23.05357
#> <= 543 42.00000 54.71768
#> <= 554 44.00000 14.87218
#> <= 599 44.00000 56.50844
#> <= 634 41.00000 39.38943
#> <= 663 42.00000 29.83273
#> <= 718 43.00000 50.22114
#> <= 770 41.00000 40.66522
#> <= 820 41.00000 33.68975
#> <= 888 41.00000 38.58097
#> <= 981 41.00000 41.78179
#> <= 1111 41.00000 42.47278
#> <= 1297 41.00000 39.19962
#> > 1297 61.00000 66.24228
#>
#> Goodness-of-fit criteria
#> Log-normal
#> Akaike's Information Criterion 17686.70
#> Bayesian Information Criterion 17696.95x_seq <- seq(0, max(degrees), length = 500)
# For plotting the no x_min version of LN
ln_fit_ccdf <- 1 - plnorm(x_seq, meanlog = degr_ln_noxmin$estimate[1], sdlog = degr_ln_noxmin$estimate[2])
# capture data that make the plot
pd1 <- plot(degr_pl, draw = F) # plot data 1, empirical distr
pd2 <- lines(degr_ln_xmin, draw = F) # plot data 2 no xmin
pd3 <- data.frame(cbind(x_seq, ln_fit_ccdf)) # plot data 3 with xmin
# now render it a ggplot
ccdfplot <- ggplot() +
geom_point(data=pd1, aes(x = x, y = y), shape=1) +
#geom_line(data=pd2, aes(x = x, y = y, color = "Log-normal fit, w/ x_min")) +
geom_line(data=pd3, aes(x = x_seq, y = ln_fit_ccdf, color = "Log-normal fit, no x_min")) +
labs(x="Extended network size", y="CCDF") +
scale_color_manual(name = "Fit", values = c(#"Log-normal fit, w/ x_min" = "green",
"Log-normal fit, no x_min" = "purple")) +
theme_bw() +
theme(legend.position = c(0.22, 0.2)) +
scale_x_log10(breaks = c(50,100,200,500,1000,2000), limits = c(min(pd1$x), max(pd1$x))) + scale_y_log10() +
ggtitle("CCDF plot of average degree")
# save
ggsave("output/ccdfplot.pdf", plot = ccdfplot, device = "pdf",
scale = 1, width = 6, height = 4, units = c("in"),
dpi = "retina")
ggsave("output/ccdfplot.jpeg", plot = ccdfplot, device = "jpeg",
scale = 1, width = 6, height = 4, units = c("in"),
dpi = "retina")
# tryout <- plot_grid(dens2, dens1, ccdfplot, nrow = 1)
#
# ggsave("output/comps_combined.pdf", plot = tryout, device = "pdf",
# scale = 1, width = 16, height = 5, units = c("in"),
# dpi = "retina")
### original plot in Base r
# # Plotting two versions of LN
# plot(degr_pl, xlab="Number of contacts", ylab="CCDF")
# lines(degr_ln_xmin, col = "green", lwd = 2)
# lines(x_seq, ln_fit_ccdf, col = "purple", lwd = 2)
# legend(x = "bottomleft",
# legend = c("Log-normal fit, w/ x_min",
# "Log-normal fit, no x_min"
# ),
# col = c("green","purple"),
# lwd = 2)
ccdfplot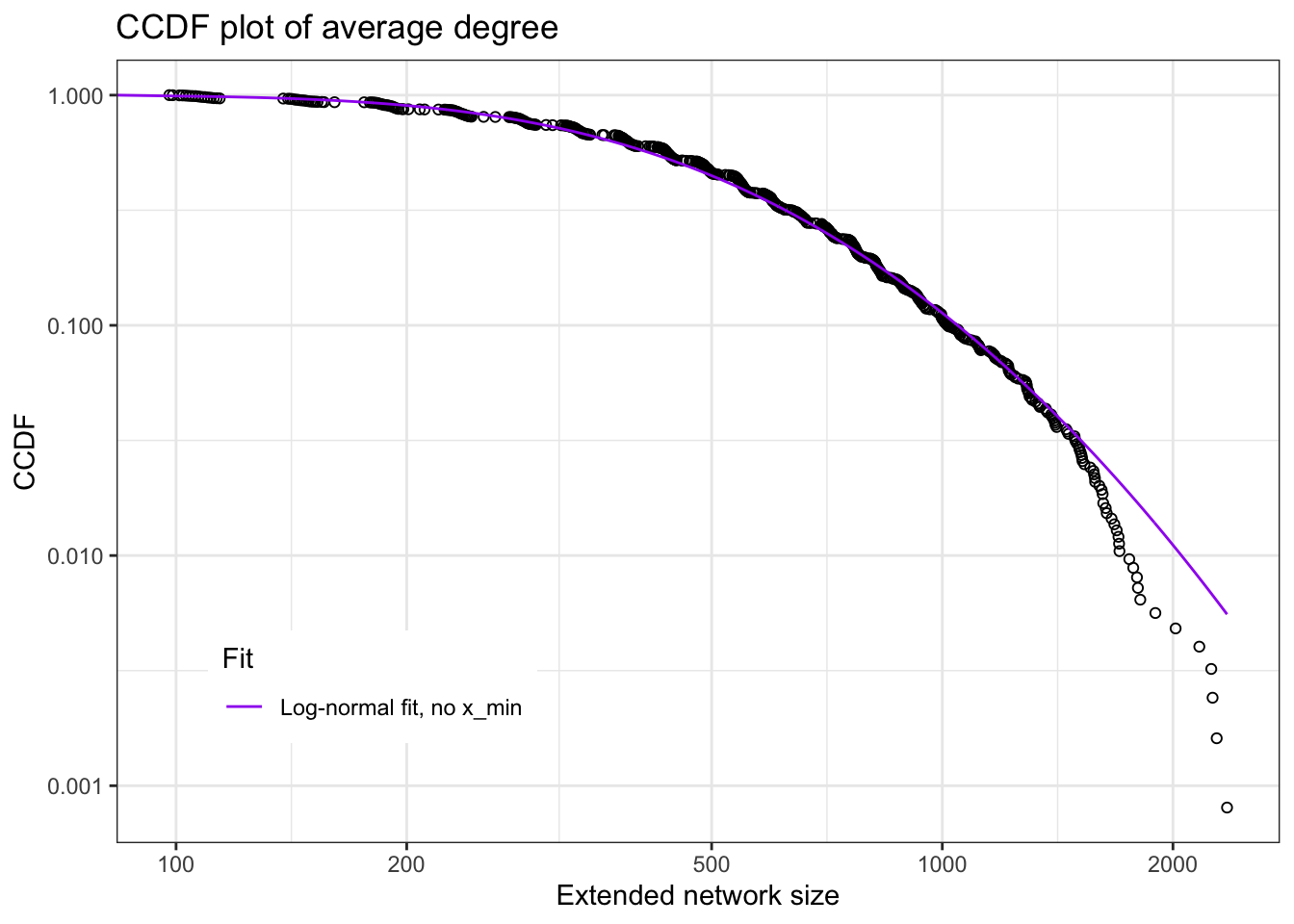
dfans <- df[, c("uni", "hbo", "mbo", "dochterzoon", "tweeling", "corona", "elauto", "scooter", "vegan",
"Sophie", "Julia", "Sanne", "Lisa", "Laura", "Maria", "Linda", "Johanna", "Monique", "Ester", "Anna",
"Elisabeth", "Cornelia", "Wilhelmina", "Amira", "Samira", "Sara", "Daan", "Sem", "Thomas", "Max",
"Kevin", "Johannes", "Dennis", "Jeroen", "Jan", "Marcel", "Cornelis", "Hendrik", "Petrus", "Willem",
"Ali", "Mohammed", "Noor")] # take mean of each of the cats
means <- colMeans(dfans)
ref1 <- c(84957, 75214, 145600, 168066, 2500, 1558549)
# ORDER: uni, hbo, mbo, dochter/zoon, tweeling, corona
ref2 <- c(273259, 460618, 261000)
# ORDER: elecauto, scooter, vegan,
ref3 <- c(15276, 16350, 27394, 21200, 25681, 334502, 29955, 266522, 39481, 2692, 136296, 110231, 112807,
98208, 1386, 2186, 11640, 22704, 13276, 40543, 17024, 23167, 307032, 36411, 49182, 186746, 35973,
134956, 118610, 86500, 102296, 4213, 5003, 4517)
# ORDER: Sophie, Julia,Sanne,Lisa,Laura,Maria,Linda,Johanna,Monique,Ester,
# Anna,Elisabeth,Cornelia,Wilhelmina,Amira,Samira,Sara,Daan,Sem,
# Thomas,Max,Kevin,Johannes,Dennis,Jeroen,Jan,Marcel,Cornelis,Hendrik,Petrus,
# Willem,Ali,Mohammed,Noor
pops <- c(ref1, ref2, ref3)
fig <- data.frame(cbind(means, pops))
cor(fig[!fig$pops > 5e+05, ])#> means pops
#> means 1.0000000 0.3410926
#> pops 0.3410926 1.0000000cor(fig[!fig$pops > 2e+05, ])#> means pops
#> means 1.0000000 0.4616083
#> pops 0.4616083 1.0000000cor(fig[fig$pops < 50000, ])#> means pops
#> means 1.0000000 0.8918255
#> pops 0.8918255 1.0000000cor(fig[fig$pops < 1e+05, ])#> means pops
#> means 1.0000000 0.3374189
#> pops 0.3374189 1.0000000ex3 <- ggplot(fig, aes(x = pops, y = means)) + geom_point() + xlim(x = c(0, 50000)) + ylim(c(0, 2.5)) +
geom_smooth(method = "lm") + geom_text(label = rownames(fig), nudge_y = 0.1) + theme_minimal() +
xlab("Population size") + ylab("Average number mentioned") + sm_statCorr() + ggtitle("C) Population size <50k")
ex3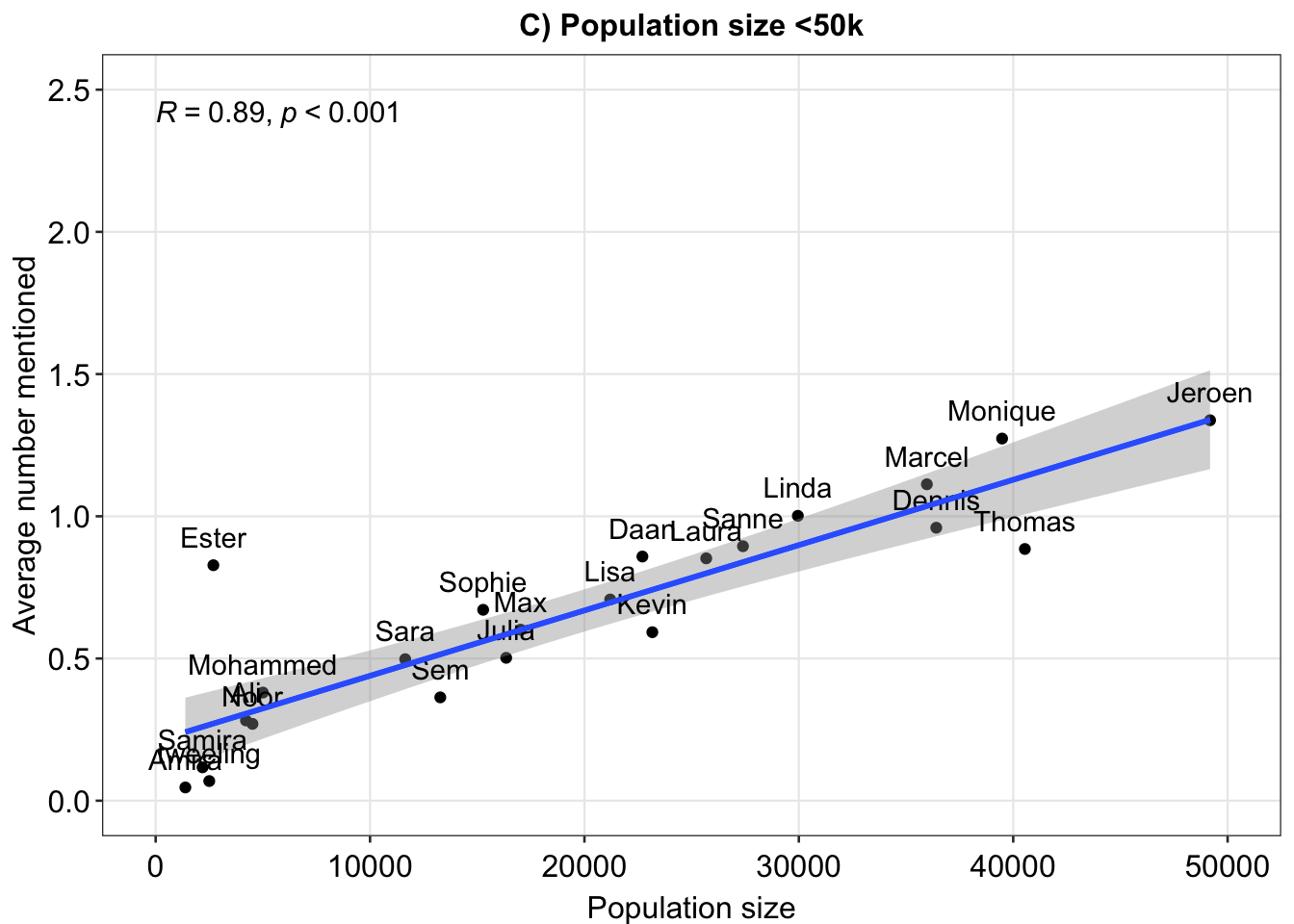
ex2 <- ggplot(fig, aes(x = pops, y = means)) + geom_point() + xlim(x = c(0, 5e+05)) + ylim(c(0, 2.5)) +
geom_smooth(method = "lm") + geom_text(label = rownames(fig), nudge_y = 0.1) + theme_minimal() +
xlab("Population size") + ylab("Average number mentioned") + sm_statCorr() + ggtitle("B) Population size <500k")
ex2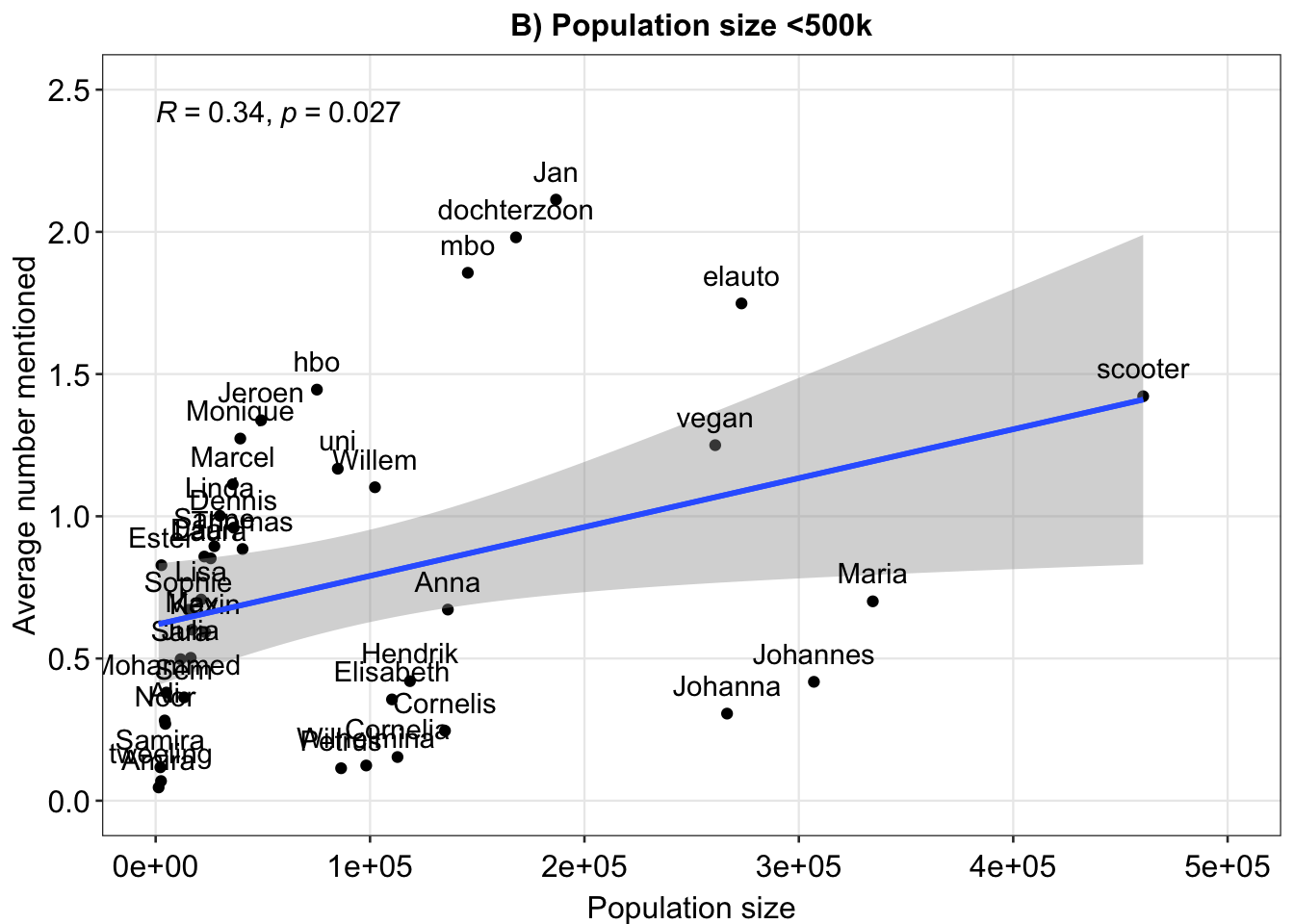
ex1 <- ggplot(fig, aes(x = pops, y = means)) + geom_point() + geom_smooth(method = "lm") + geom_text(label = rownames(fig),
nudge_y = 0.1) + theme_minimal() + xlab("Population size") + ylab("Average number mentioned") + sm_statCorr() +
ggtitle("A) All population sizes")
ex1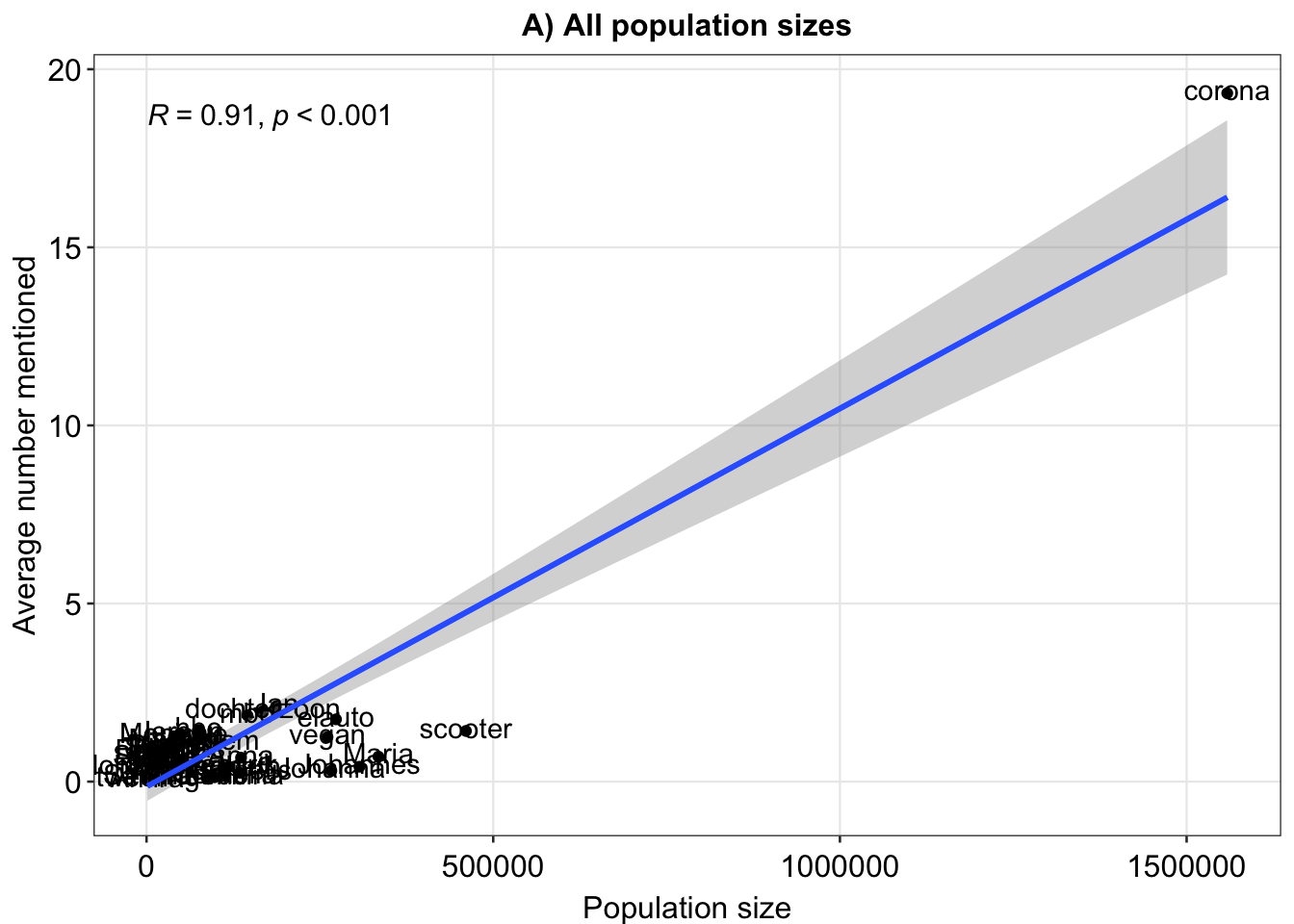
ex <- cowplot::plot_grid(ex1, ex2, ex3, nrow = 1)
ggsave("output/popsizes.pdf", plot = ex, device = "pdf", scale = 1, width = 16, height = 5, units = c("in"),
dpi = "retina")
ggsave("output/popsizes.jpeg", plot = ex, device = "jpeg", scale = 1, width = 16, height = 5, units = c("in"),
dpi = "retina")
ex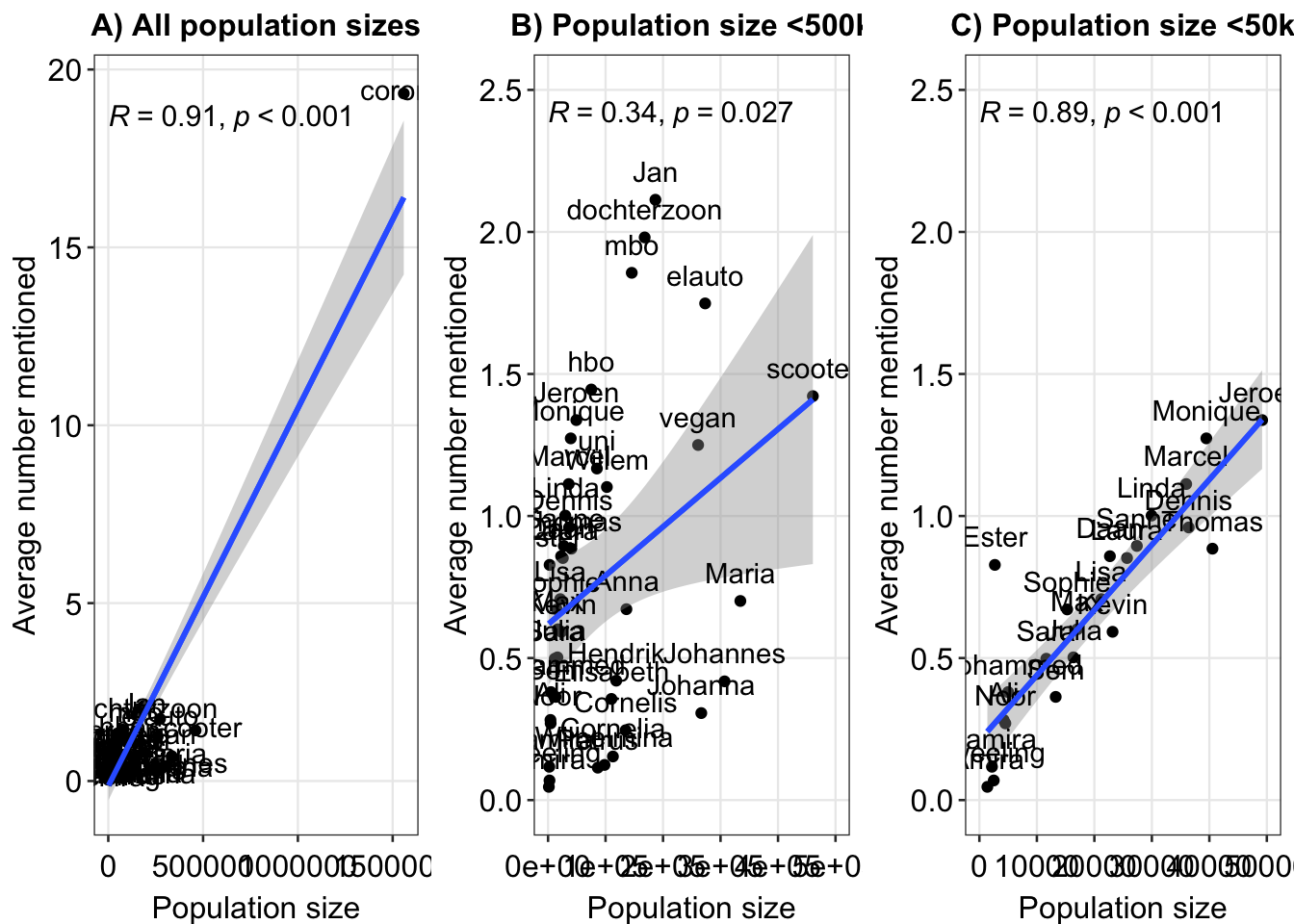
Ci0tLQp0aXRsZTogIkRlc2NyaXB0aXZlIGFuYWx5c2VzIgojYmlibGlvZ3JhcGh5OiByZWZlcmVuY2VzLmJpYgphdXRob3I6ICJCYXMgSG9mc3RyYSIKLS0tCgpgYGB7ciwgZ2xvYmFsc2V0dGluZ3MsIGVjaG89RkFMU0UsIHdhcm5pbmc9RkFMU0UsIHJlc3VsdHM9J2hpZGUnfQpsaWJyYXJ5KGtuaXRyKQoKa25pdHI6Om9wdHNfY2h1bmskc2V0KGVjaG8gPSBUUlVFKQpvcHRzX2NodW5rJHNldCh0aWR5Lm9wdHM9bGlzdCh3aWR0aC5jdXRvZmY9MTAwKSx0aWR5PVRSVUUsIHdhcm5pbmcgPSBGQUxTRSwgbWVzc2FnZSA9IEZBTFNFLGNvbW1lbnQgPSAiIz4iLCBjYWNoZT1UUlVFLCBjbGFzcy5zb3VyY2U9YygidGVzdCIpLCBjbGFzcy5vdXRwdXQ9YygidGVzdDIiKSkKb3B0aW9ucyh3aWR0aCA9IDEwMCkKcmdsOjpzZXR1cEtuaXRyKCkKCgoKY29sb3JpemUgPC0gZnVuY3Rpb24oeCwgY29sb3IpIHtzcHJpbnRmKCI8c3BhbiBzdHlsZT0nY29sb3I6ICVzOyc+JXM8L3NwYW4+IiwgY29sb3IsIHgpIH0KCmBgYAoKYGBge3Iga2xpcHB5LCBlY2hvPUZBTFNFLCBpbmNsdWRlPVRSVUV9CmtsaXBweTo6a2xpcHB5KHBvc2l0aW9uID0gYygndG9wJywgJ3JpZ2h0JykpCiNrbGlwcHk6OmtsaXBweShjb2xvciA9ICdkYXJrcmVkJykKI2tsaXBweTo6a2xpcHB5KHRvb2x0aXBfbWVzc2FnZSA9ICdDbGljayB0byBjb3B5JywgdG9vbHRpcF9zdWNjZXNzID0gJ0RvbmUnKQpgYGAKCkxhc3QgY29tcGlsZWQgb24gYHIgZm9ybWF0KFN5cy50aW1lKCksICclQiwgJVknKWAKCjxicj4KCi0tLS0KClRoaXMgaXMgdGhlIGNvZGUgd2l0aCB3aGljaCB3ZSByZW5kZXIgb3VyIGRlc2NyaXB0aXZlIGFuYWx5c2VzCgo8YnI+CgotLS0tCgojIEluaXRhdGlhdGluZyBSIGVudmlyb25tZW50CgpTdGFydCBvdXQgd2l0aCBhIGN1c3RvbSBmdW5jdGlvbiB0byBsb2FkIGEgc2V0IG9mIHJlcXVpcmVkIHBhY2thZ2VzLgogIApgYGB7ciBwYWNrLCBldmFsPVRSVUV9CiMgcGFja2FnZXMgYW5kIHJlYWQgZGF0YQpybShsaXN0ID0gbHMoKSkKCiMgKGMpIEpvY2hlbSBUb2xzbWEKZnBhY2thZ2UuY2hlY2sgPC0gZnVuY3Rpb24ocGFja2FnZXMpIHsKICBsYXBwbHkocGFja2FnZXMsIEZVTiA9IGZ1bmN0aW9uKHgpIHsKICAgIGlmICghcmVxdWlyZSh4LCBjaGFyYWN0ZXIub25seSA9IFRSVUUpKSB7CiAgICAgIGluc3RhbGwucGFja2FnZXMoeCwgZGVwZW5kZW5jaWVzID0gVFJVRSwgcmVwb3MgPSAiaHR0cDovL2NyYW4udXMuci1wcm9qZWN0Lm9yZyIpCiAgICAgIGxpYnJhcnkoeCwgY2hhcmFjdGVyLm9ubHkgPSBUUlVFKQogICAgfQogIH0pCn0KcGFja2FnZXMgPSBjKCJoYXZlbiIsICJjb2RhIiwgIm1hdHJpeFN0YXRzIiwgInBhcmFsbGVsIiwgIk1BU1MiLCAiZG9QYXJhbGxlbCIsICJkcGx5ciIsICJjb3dwbG90IiwgCiAgICAgICAgICAgICAidGlkeXZlcnNlIiwgIm5hbmlhciIsICJkb3R3aGlza2VyIiAsImd0IiwgInJlc2hhcGUyIiwgIlZHQU0iLCAiZXhwc3MiLCAiSG1pc2MiLAogICAgICAgICAgICAgInBvd2VSbGF3IiwgImZpdGRpc3RycGx1cyIsICJncmlkIiwgImdncGxvdGlmeSIsICJzbXBsb3QyIikKZnBhY2thZ2UuY2hlY2socGFja2FnZXMpCnJtKHBhY2thZ2VzKQpsb2FkKCJkYXRhL2R1dGNoX25ldHNpemVfYW5hbHlzZXNfcmV2aXNpb25fMi5yZGEiKQpgYGAKPGJyPgoKLS0tLQoKIyBEZXNjcmlwdGl2ZXMgaW5kZXBlbmRlbnQgdmFyaWFibGVzCgpUaGUgY29kZSBiZWxvdyBnZW5lcmF0ZXMgdGhlIGRlc2NyaXB0aXZlIHZhbHVlcyB3aGljaCBhcmUgdXNlZCBmb3IgVGFibGVzIDEgYW5kIDIuCiAgCgpgYGB7ciBkZXNjaW5kLCBldmFsID0gVFJVRX0KCiMgZGVzY3JpcHRpdmUgdGFibGUgbm90IGF1dG9tYXRlZDogVEFCTEUgMQp0YWJsZShkZiR3b3JrKQpwc3ljaDo6ZGVzY3JpYmUoZGYkd29yaykKcHN5Y2g6OmRlc2NyaWJlKGRmJGhoc2l6ZSkKCnRhYmxlKGRmJGFnZWNhdCkKCgojIDEgTWFqCiMgMiB3ZXN0CiMgMyBub253ZXN0CgoKdGFibGUoZGYkaW5jb21lKQojIDEgPCBtb2RhbAojIDIgPiBtb2RhbAojIDMgdW5rbm93bgoKcHN5Y2g6OmRlc2NyaWJlKGRmJHdvcnRoaG91c2UpCgoKdGFibGUoZGYkd29tYW4pCnBzeWNoOjpkZXNjcmliZShkZiR3b21hbikKCgoKdGFibGUoZGYkb3BsMikKc3VtbWFyeShkZiRvcGwyKQojIDEgcHJpbS9zZWMKIyAyIGxvd2VyIHRlcnQKIyAzIGhpZ2hlciB0ZXJ0CgojcHN5Y2g6OmRlc2NyaWJlKGRmJG5laWdoZGVucykKCgojIHRoaXMgaXMgZm9yIHRoZSBjb3JyZWxhdGlvbiB0YWJsZQojZGYkZWR1YzMgPC0gZGYkb3BsCiNkZiRlZHVjMyA8LSBhcy5udW1lcmljKGFzLmNoYXJhY3RlcihkZiRlZHVjMykpCgp0YWJsZShkZiRtaWdyMykKCiNjb3IoYXMubWF0cml4KGRmW2RmJGluY29tZSE9MyxjKCJpbmNvbWUiLCJ3b3J0aGhvdXNlIildKSkKCiNyY29ycihhcy5tYXRyaXgoZGZbLGMoIndvcmsiLCAiaGhzaXplIiwgImxlZWZ0aWpkMTAiLCAid29tYW4iLCAiZWR1YzMiLCAibmVpZ2hkZW5zIiwgIndvcnRoaG91c2UiICldKSwgdHlwZSA9ICJwZWFyc29uIikKCmBgYAoKPGJyPgoKYGBge3IgdGFibGVob21vZ2VuZWl0eSwgZXZhbCA9IFRSVUV9CiMgdGFibGUgMgpzdW1tYXJ5KGRmJHBlcndvbWVuKQpzdW1tYXJ5KGRmW2RmJHdvbWFuID09IDEsIGMoInBlcndvbWVuIildKQpzdW1tYXJ5KGRmW2RmJHdvbWFuID09IDAsIGMoInBlcndvbWVuIildKQoKc3VtbWFyeShkZiRwZXJtZW4pCnN1bW1hcnkoZGZbZGYkd29tYW4gPT0gMSwgYygicGVybWVuIildKQpzdW1tYXJ5KGRmW2RmJHdvbWFuID09IDAsIGMoInBlcm1lbiIpXSkKCnN1bW1hcnkoZGYkc2FtZWdlbmRlcikKc3VtbWFyeShkZltkZiR3b21hbiA9PSAxLCBjKCJzYW1lZ2VuZGVyIildKQpzdW1tYXJ5KGRmW2RmJHdvbWFuID09IDAsIGMoInNhbWVnZW5kZXIiKV0pCgpzdW1tYXJ5KGRmJHBlcmVkdWNoaWdoKQpzdW1tYXJ5KGRmW2RmJG9wbDIgPT0gMSwgYygicGVyZWR1Y2hpZ2giKV0pCnN1bW1hcnkoZGZbZGYkb3BsMiA9PSAwLCBjKCJwZXJlZHVjaGlnaCIpXSkKCnN1bW1hcnkoZGYkcGVyZWR1Y2xvdykKc3VtbWFyeShkZltkZiRvcGwyID09IDEsIGMoInBlcmVkdWNsb3ciKV0pCnN1bW1hcnkoZGZbZGYkb3BsMiA9PSAwLCBjKCJwZXJlZHVjbG93IildKQoKc3VtbWFyeShkZiRzYW1lZWR1YykKc3VtbWFyeShkZltkZiRvcGwyID09IDEsIGMoInNhbWVlZHVjIildKQpzdW1tYXJ5KGRmW2RmJG9wbDIgPT0gMCwgYygic2FtZWVkdWMiKV0pCgpzdW1tYXJ5KGRmJG5ldHNvdmVyNikKCmBgYAoKLS0tLQoKIyBDb21wYXJpbmcgbmFpdmUgZXN0aW1hdGlvbnMKClRoZSBjb2RlIGJlbG93IGdlbmVyYXRlcyBGaWd1cmUgMSBmcm9tIHRoZSBwYXBlciBhbmQgcnVucyBhIG51bWJlciBvZiBjb3JyZWxhdGlvbnMgZm91bmQgb24gcGFnZSBYLgogIAoKYGBge3IgbmFpY29tcHMsIGV2YWwgPSBUUlVFfQojIAojIGNvbXBzIDwtIGdhdGhlcihkZlssIGMoIm5zaXplX25haXZlIiwgIm5zaXplX2IxYjIiLCAibnNpemVfYjMiLCAibnNpemVfbjEiLCAibnNpemVfbjIiLCAibnNpemVfbjMiLCAibnNpemVfbjEyMyIpXSkKIyAKIyBjb21wYXJpc29ucyA8LSBnZ3Bsb3QoY29tcHNbY29tcHMkdmFsdWUgPCAyMDAwLCBdLCBhZXMoeD12YWx1ZSwgY29sb3IgPSBrZXkpKSArIAojICAgZ2VvbV9kZW5zaXR5KHNpemUgPSAwLjUpICsgCiMgICB0aGVtZV9taW5pbWFsKCkgKwojICAgbGFicyh4ID0gIk5ldHdvcmsgc2l6ZSBlc3RpbWF0ZSIsIHkgPSAiRGVuc2l0eSIpICsKIyAgIHNjYWxlX2NvbG9yX21hbnVhbChuYW1lID0gIkVzdGltYXRpb24gc2NlbmFyaW8iLCAKIyAgICAgICAgICAgICAgICAgICAgICAgYnJlYWtzID0gYygibnNpemVfbmFpdmUiLCAibnNpemVfYjFiMiIsICJuc2l6ZV9iMyIsICJuc2l6ZV9uMSIsICJuc2l6ZV9uMiIsICJuc2l6ZV9uMyIsICJuc2l6ZV9uMTIzIiksIAojICAgICAgICAgICAgICAgICAgICAgICAgbGFiZWxzID0gYygiTmFpdmUgZXN0aW1hdG9yOiBhbGwgWCdzIiwgCiMgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICJCYXR0ZXJ5IDE6IFRlcnQuIGVkdWMuLCBlbGVjIHZlaGljbGUsIGV0Yy4iLCAKIyAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIkJhdHRlcnkgMjogYWxsIG5hbWVzIiwgCiMgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICJOYW1lcyAxOiBTb3BoaWUsIEFubmEsIFRob21hcywgV2lsbGVtIiwgCiMgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICJOYW1lcyAyOiBKdWxpYSwgRWxpc2FiZXRoLCBNYXgsIEFsaSIsCiMgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICJOYW1lcyAzOiBTYW5uZSwgQ29ybmVsaWEsIEtldmluLCBNb2hhbW1lZCIsCiMgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICJOYW1lczErMiszIiksCiMgICAgICAgICAgICAgICAgICAgICAgdmFsdWVzID0gYygiIzAwMDAwMCIsICIjRTY5RjAwIiwgIiM1NkI0RTkiLCAiIzAwOUU3MyIsIAojICAgICAgICAgICAgICAgICAgICAgICAgICAgIiMwMDcyQjIiLCAiI0Q1NUUwMCIsICIjQ0M3OUE3IiwgImRhcmtncmV5IikpCiMgCiMgIyBzYXZlCiMgZ2dzYXZlKCJvdXRwdXQvY29tcGFyaXNvbnMucGRmIiwgcGxvdCA9IGNvbXBhcmlzb25zLCBkZXZpY2UgPSAicGRmIiwKIyAgICAgICAgc2NhbGUgPSAxLCB3aWR0aCA9IDEwLCBoZWlnaHQgPSA1LjUsIHVuaXRzID0gYygiaW4iKSwKIyAgICAgICAgZHBpID0gInJldGluYSIpCiMgCiMgCiMgCiMgIyAjIGNvcnJlbGF0aW9uIGJhdHRlcnkgMSBhbmQgMgojICMgY29yKGRmJG5zaXplX2IxLCBkZiRuc2l6ZV9iMikKIyAjIAojICMgIyBjb3JyZWxhdGlvbiBiYXR0ZXJ5IDEgYW5kIGFsbAojICMgY29yKGRmJG5zaXplX2IxLCBkZiRuc2l6ZV9uYWl2ZSkKIyAKIyAjIGNvcnJlbGF0aW9uIGJhdHRlcnkgMSsyIGFuZCBhbGwKIyBjb3IoZGYkbnNpemVfYjFiMiwgZGYkbnNpemVfbmFpdmUpCiMgCiMgIyBjb3JyZWxhdGlvbiBiYXR0ZXJ5IDMgKG5hbWVzKSBhbmQgYWxsCiMgY29yKGRmJG5zaXplX2IzLCBkZiRuc2l6ZV9uYWl2ZSkKIyAKIyAjIGNvcnJlbGF0aW9uIG5hbWVzIDEgYW5kIGFsbAojIGNvcihkZiRuc2l6ZV9uMSwgZGYkbnNpemVfbmFpdmUpCiMgCiMgIyBjb3JyZWxhdGlvbiBuYW1lcyAyIGFuZCBhbGwKIyBjb3IoZGYkbnNpemVfbjIsIGRmJG5zaXplX25haXZlKQojIAojICMgY29ycmVsYXRpb24gbmFtZXMgMyBhbmQgYWxsCiMgY29yKGRmJG5zaXplX24zLCBkZiRuc2l6ZV9uYWl2ZSkKIyAKIyAjIGNvcnJlbGF0aW9uIG5hbWVzIDEyMyBhbmQgYWxsCiMgY29yKGRmJG5zaXplX24xMjMsIGRmJG5zaXplX25haXZlKQojIAojICMgc2FtcGxlIDUgY29sdW1ucyBvZiBzY2VuYXJpb3MgYW5kIGNvcnJlbGF0ZSB3aXRoIG5haXZlIGVzdGltYW5kCiMgc2V0LnNlZWQoMTk4NykKIyBzYW1wbGUoMTM6MTgzLCA1KQojIAojICMgY29ycmVsYXRpb24gc2NlbmFyaW8gODUgYW5kIG5haXZlCiMgY29yKGRmJG5zaXplX25haXZlLCBkZlssIDg1XSkKIyAKIyAjIGNvcnJlbGF0aW9uIHNjZW5hcmlvIDM2IGFuZCBuYWl2ZQojIGNvcihkZiRuc2l6ZV9uYWl2ZSwgZGZbLCAzNl0pCiMgCiMgIyBjb3JyZWxhdGlvbiBzY2VuYXJpbyAxNTAgYW5kIG5haXZlCiMgY29yKGRmJG5zaXplX25haXZlLCBkZlssIDE1MF0pCiMgCiMgIyBjb3JyZWxhdGlvbiBzY2VuYXJpbyAxNCBhbmQgbmFpdmUKIyBjb3IoZGYkbnNpemVfbmFpdmUsIGRmWywgMTRdKQojIAojICMgY29ycmVsYXRpb24gc2NlbmFyaW8gMTI1IGFuZCBuYWl2ZQojIGNvcihkZiRuc2l6ZV9uYWl2ZSwgZGZbLCAxMjVdKQojIAojIGNvbXBhcmlzb25zCgpgYGAKCgoKCjxicj4KCi0tLS0KCiMgQ29tcGFyaW5nIEJheWVzaWFuIGVzdGltYXRpb25zCgpUaGUgY29kZSBiZWxvdyBnZW5lcmF0ZXMgRmlndXJlIDIgZnJvbSB0aGUgcGFwZXIgYXNzb2NpYXRlZCB3aXRoIHRoZSB0ZXh0IG9uIHBhZ2UgWC4KICAKYGBge3IgYmF5ZWNvbXBzLCBldmFsID0gVFJVRX0KIyAKIyBuZXRzaXplcyA8LSByZWFkLnRhYmxlKGZpbGUgPSAiZGF0YS9kdXRjaF9uZXRzaXplX2Rlc2MudHh0IikKIyAKIyAjIFZJWiBvZiBuZXRzaXplCiMgbmV0c2l6ZV9sIDwtIGdhdGhlcihuZXRzaXplcykKIyBkZW5zMSA8LSBnZ3Bsb3QobmV0c2l6ZV9sW25ldHNpemVfbCR2YWx1ZSA8IDIwMDAsXSwgYWVzKHg9dmFsdWUsIGNvbG9yID0ga2V5KSkgKyAKIyAgIGdlb21fZGVuc2l0eShhbHBoYSA9IC4yLCBzaXplID0gMC4xKSArIAojICAgdGhlbWVfbWluaW1hbCgpICsgCiMgICB0aGVtZShsZWdlbmQucG9zaXRpb24gPSAibm9uZSIpICsKIyAgIGxhYnMoeCA9ICJOZXR3b3JrIHNpemUgZXN0aW1hdGUiLCB5ID0gIkRlbnNpdHkiKSArCiMgICBnZW9tX3ZsaW5lKHhpbnRlcmNlcHQ9YXMubnVtZXJpYyhwc3ljaDo6ZGVzY3JpYmUobmV0c2l6ZV9sWywgMl0pWzNdKSwgY29sb3IgPSAiZGFya2dyZXkiLCBsaW5ldHlwZSA9IDIpICsKIyAgIGdlb21fdmxpbmUoeGludGVyY2VwdD1hcy5udW1lcmljKHBzeWNoOjpkZXNjcmliZShuZXRzaXplX2xbLCAyXSlbNV0pLCBjb2xvciA9ICJkYXJrZ3JleSIsIGxpbmV0eXBlID0gMikgKwojICAgYW5ub3RhdGUoInRleHQiLCB4ID0gNDkwLCB5ID0gMC4wMDA0LCBjb2xvciA9ICJkYXJrZ3JleSIsIGFuZ2xlID0gOTAsIAojICAgICAgICAgICAgbGFiZWwgPSBwYXN0ZTAoIk1lYW4gPSAiLCByb3VuZChhcy5udW1lcmljKHBzeWNoOjpkZXNjcmliZShuZXRzaXplX2xbLCAyXSlbM10pLCBkaWdpdHMgPSAwKSkpICsKIyAgIGFubm90YXRlKCJ0ZXh0IiwgeCA9IDM0MCwgeSA9IDAuMDAwNCwgY29sb3IgPSAiZGFya2dyZXkiLCBhbmdsZSA9IDkwLCAKIyAgICAgICAgICAgIGxhYmVsID0gcGFzdGUwKCJNZWRpYW4gPSAiLCByb3VuZChhcy5udW1lcmljKHBzeWNoOjpkZXNjcmliZShuZXRzaXplX2xbLCAyXSlbNV0pLCBkaWdpdHMgPSAwKSkpICsKIyAgIGdndGl0bGUoIkIpIERpc3RyaWJ1dGlvbiBvZiBuZXR3b3JrIHNpemVzLCBhbGwgc2NlbmFyaW9zIikKIyAKIyAKIyAjIEdldCBsb3dlciB0cmlhbmdsZSBvZiB0aGUgY29ycmVsYXRpb24gbWF0cml4CiMgZ2V0X2xvd2VyX3RyaTwtZnVuY3Rpb24oY29ybWF0KXsKIyAgIGNvcm1hdFt1cHBlci50cmkoY29ybWF0KV0gPC0gTkEKIyAgIHJldHVybihjb3JtYXQpCiMgfQojIG1hdCA8LSBjb3IobmV0c2l6ZXMpCiMgbG93ZXJfdHJpIDwtIGdldF9sb3dlcl90cmkobWF0KQojIG1lbHRlZF9jb3JtYXQgPC0gcmVzaGFwZTI6Om1lbHQobG93ZXJfdHJpKSAjIGRhdGEudGFibGUgYWxzbyBoYXMgbWVsdCBmdW5jaXRvbiB0aGF0IHdvbid0IHdvcmsgb24gbWF0cmljZXMKIyBtZWx0ZWRfY29ybWF0JFZhcjIgPC0gYXMuY2hhcmFjdGVyKG1lbHRlZF9jb3JtYXQkVmFyMikKIyBtZWx0ZWRfY29ybWF0JFZhcjEgPC0gYXMuY2hhcmFjdGVyKG1lbHRlZF9jb3JtYXQkVmFyMSkKIyBtZWx0ZWRfY29ybWF0IDwtIG1lbHRlZF9jb3JtYXRbIW1lbHRlZF9jb3JtYXQkVmFyMiA9PSBtZWx0ZWRfY29ybWF0JFZhcjEsXQojIG1lbHRlZF9jb3JtYXQgPC0gbWVsdGVkX2Nvcm1hdFshaXMubmEobWVsdGVkX2Nvcm1hdCR2YWx1ZSksIF0KIyAKIyAjIFZpeiBvZiBjb3JyZWxhdGlvbnMgYmV0d2VlbiBuZXRzaXplIGVzdGltYXRlcwojIGRlbnMyIDwtIGdncGxvdChtZWx0ZWRfY29ybWF0LCBhZXMoeD12YWx1ZSkpICsgCiMgICBnZW9tX2RlbnNpdHkoc2l6ZSA9IDAuMykgKyAKIyAgIHhsaW0oMC45MTUsIDEpICsgCiMgICB0aGVtZV9taW5pbWFsKCkgKyAKIyAgIGxhYnMoeD0iUGVhcnNvbiBjb3JyZWxhdGlvbiIsIHkgPSAiRGVuc2l0eSIpICsKIyAgIGdlb21fdmxpbmUoeGludGVyY2VwdCA9IC45NSwgY29sb3IgPSAiZGFya2dyZXkiLCBsaW5ldHlwZSA9IDIpICsKIyAgIGdndGl0bGUoIkEpIERpc3RyaWJ1dGlvbnMgb2YgY29ycmVsYXRpb25zIGJldHdlZW4gbmV0d29yayBzaXplIHNjZW5hcmlvcyIpICArCiMgICBnZW9tX3NlZ21lbnQoeCA9IDAuOTUsIHkgPSAxMjUsIHhlbmQgPSAuOTksIHllbmQgPSAxMjUsIGxpbmV0eXBlID0gMiwgY29sb3IgPSAiZGFya2dyZXkiLAojICAgICAgICAgICAgICAgICBhcnJvdyA9IGFycm93KGxlbmd0aCA9IHVuaXQoMC4yNSwgImNtIikpKSAgKwojICAgYW5ub3RhdGUoInRleHQiLCB4ID0gLjk3LCB5ID0gMTM1LCBjb2xvciA9ICJkYXJrZ3JleSIsIGFuZ2xlID0gMCwgCiMgICAgICAgICAgICBsYWJlbCA9IHBhc3RlMChyb3VuZChucm93KG1lbHRlZF9jb3JtYXRbbWVsdGVkX2Nvcm1hdCR2YWx1ZSA+IC45NSwgXSkvbnJvdyhtZWx0ZWRfY29ybWF0KSoxMDAsIGRpZ2l0cyA9IDEpLCIlIG9mIGNvcnJlbGF0aW9ucyBhcmUgPiAuOTUiKSkKIyAKIyAjIGxheSAnbSBvdXQgb24gdGhlIGdyaWQgICAgICAgICAgIAojIGRlbnNlcyA8LSBwbG90X2dyaWQoZGVuczIsIGRlbnMxLCBucm93ID0gMSkgCiMgCiMgIyBzYXZlCiMgZ2dzYXZlKCJvdXRwdXQvZGVuc2l0aWVzLnBkZiIsIHBsb3QgPSBkZW5zZXMsIGRldmljZSA9ICJwZGYiLAojICAgICAgICBzY2FsZSA9IDEsIHdpZHRoID0gMTIsIGhlaWdodCA9IDQsIHVuaXRzID0gYygiaW4iKSwKIyAgICAgICAgZHBpID0gInJldGluYSIpCiMgCiMgIyBkZW5zZXMKYGBgCgo8YnI+CgotLS0tCgoKIAojIEZpZ3VyZSAxCgpUaGUgY29kZSBiZWxvdyBnZW5lcmF0ZXMgRmlndXJlIDEgZnJvbSB0aGUgcGFwZXIgYXNzb2NpYXRlZCB3aXRoIHRoZSB0ZXh0IG9uIHBhZ2UgWC4KICAKYGBge3IgZGVuc2l0eXJldmlzaW9uLCBldmFsID0gVFJVRX0KCm5ldHNpemVfbCA8LSBkYXRhLmZyYW1lKGRmWywgYygibmV0c292ZXI2IildKQpuYW1lcyhuZXRzaXplX2wpIDwtIGMoInZhbHVlIikKcm91bmQoc3VtbWFyeShkZiRuZXRzb3ZlcjYpWzNdLCBkaWdpdHMgPSAwKQpyb3VuZChzdW1tYXJ5KGRmJG5ldHNvdmVyNilbNF0sIGRpZ2l0cyA9IDApCklRUihkZiRuZXRzb3ZlcjYpCgpkZW5zMSA8LSBnZ3Bsb3QobmV0c2l6ZV9sLCBhZXMoeD12YWx1ZSkpICsgCiAgZ2VvbV9kZW5zaXR5KGFscGhhID0gLjIsIHNpemUgPSAwLjUpICsgCiAgdGhlbWVfbWluaW1hbCgpICsgCiAgdGhlbWUobGVnZW5kLnBvc2l0aW9uID0gIm5vbmUiKSArCiAgbGFicyh4ID0gIk5ldHdvcmsgc2l6ZSBlc3RpbWF0ZSIsIHkgPSAiRGVuc2l0eSIpICsKICBzY2FsZV9jb2xvcl9tYW51YWwodmFsdWVzID0gYygiIzU2QjRFOSIpKSArCiAgICBnZW9tX3ZsaW5lKHhpbnRlcmNlcHQ9NDg4LCBjb2xvciA9ICJkYXJrZ3JleSIsIGxpbmV0eXBlID0gMikgKwogIGdlb21fdmxpbmUoeGludGVyY2VwdD01NjgsIGNvbG9yID0gImRhcmtncmV5IiwgbGluZXR5cGUgPSAyKSArCiAgYW5ub3RhdGUoInRleHQiLCB4ID0gNjMwLCB5ID0gMC4wMDA0LCBjb2xvciA9ICJibGFjayIsIGFuZ2xlID0gOTAsIAogICAgICAgICAgIGxhYmVsID0gIk1lYW4gPSA1NjgiKSArCiAgYW5ub3RhdGUoInRleHQiLCB4ID0gMzYwLCB5ID0gMC4wMDA0LCBjb2xvciA9ICJibGFjayIsIGFuZ2xlID0gOTAsIAogICAgICAgICAgIGxhYmVsID0gIk1lZGlhbiA9IDQ4OCIpICsKICB4bGltKGMoMCwgMjUwMCkpIAoKZ2dzYXZlKCJvdXRwdXQvZGVuc2l0aWVzMV9yZXZpc2lvbi5wZGYiLCBwbG90ID0gZGVuczEsIGRldmljZSA9ICJwZGYiLAogICAgICAgc2NhbGUgPSAxLCB3aWR0aCA9IDUsIGhlaWdodCA9IDQsIHVuaXRzID0gYygiaW4iKSwKICAgICAgIGRwaSA9ICJyZXRpbmEiKQpnZ3NhdmUoIm91dHB1dC9kZW5zaXRpZXMxX3JldmlzaW9uLmpwZWciLCBwbG90ID0gZGVuczEsIGRldmljZSA9ICJqcGVnIiwKICAgICAgIHNjYWxlID0gMSwgd2lkdGggPSA1LCBoZWlnaHQgPSA0LCB1bml0cyA9IGMoImluIiksCiAgICAgICBkcGkgPSAicmV0aW5hIikKCgpjb3IoZGZbLCBjKCJuZXRzb3ZlcjEiLCAibmV0c292ZXIyIiwgIm5ldHNvdmVyNCIsICJuZXRzb3ZlcjUiLCAibmV0c292ZXI2IildKQojIAojICMgVklaIG9mIG5ldHNpemUgc2NlbmFyaW9zCiMgbmV0c2l6ZV9sIDwtIGdhdGhlcihkZlssIGMoIm5ldHNvdmVyMSIsICJuZXRzb3ZlcjIiLCAibmV0c292ZXI0IiwgIm5ldHNvdmVyNSIsICJuZXRzb3ZlcjYiKV0pCiMgcm91bmQoc3VtbWFyeShkZiRuZXRzb3ZlcjYpWzNdLCBkaWdpdHMgPSAwKQojIHJvdW5kKHN1bW1hcnkoZGYkbmV0c292ZXI2KVs0XSwgZGlnaXRzID0gMCkKIyAKIyBkZW5zMiA8LSBnZ3Bsb3QobmV0c2l6ZV9sLCBhZXMoeD12YWx1ZSwgY29sb3IgPSBrZXkpKSArCiMgICBnZW9tX2RlbnNpdHkoYWxwaGEgPSAuMiwgc2l6ZSA9IDAuNSkgKwojICAgdGhlbWVfbWluaW1hbCgpICsKIyAgIHRoZW1lKGxlZ2VuZC5wb3NpdGlvbiA9ICJub25lIikgKwojICAgbGFicyh4ID0gIk5ldHdvcmsgc2l6ZSBlc3RpbWF0ZSIsIHkgPSAiRGVuc2l0eSIpICsKIyAgIHNjYWxlX2NvbG9yX21hbnVhbCh2YWx1ZXMgPSBjKCJncmV5IiwgImdyZXkiLCAiZ3JleSIsICJncmV5IiwgIiM1NkI0RTkiKSkgKwojICAgICBnZW9tX3ZsaW5lKHhpbnRlcmNlcHQ9NDg4LCBjb2xvciA9ICJkYXJrZ3JleSIsIGxpbmV0eXBlID0gMikgKwojICAgZ2VvbV92bGluZSh4aW50ZXJjZXB0PTU2OCwgY29sb3IgPSAiZGFya2dyZXkiLCBsaW5ldHlwZSA9IDIpICsKIyAgIGFubm90YXRlKCJ0ZXh0IiwgeCA9IDU2MCwgeSA9IDAuMDAwOCwgY29sb3IgPSAiYmxhY2siLCBhbmdsZSA9IDkwLAojICAgICAgICAgICAgbGFiZWwgPSAiTWVhbiA9IDU2OCIpICsKIyAgIGFubm90YXRlKCJ0ZXh0IiwgeCA9IDQwMCwgeSA9IDAuMDAwOCwgY29sb3IgPSAiYmxhY2siLCBhbmdsZSA9IDkwLAojICAgICAgICAgICAgbGFiZWwgPSAiTWVkaWFuID0gNDg4IikgKwojICAgeGxpbShjKDAsIDI1MDApKQojICMgc2F2ZQojIGdnc2F2ZSgib3V0cHV0L2RlbnNpdGllczJfcmV2aXNpb24ucGRmIiwgcGxvdCA9IGRlbnMxLCBkZXZpY2UgPSAicGRmIiwKIyAgICAgICAgc2NhbGUgPSAxLCB3aWR0aCA9IDUsIGhlaWdodCA9IDQsIHVuaXRzID0gYygiaW4iKSwKIyAgICAgICAgZHBpID0gInJldGluYSIpCiMgZGVuczIKCgoKCgpgYGAKCgojIERpc3RyaWJ1dGlvbmFsIGZpdAoKV2Ugbm93IGZpdCBhICJjb21wbGVtZW50YXJ5IGN1bXVsYXRpdmUgZGVncmVlIGRpc3RyaWJ1dGlvbiIgYW5kIGNoZWNrIGhvdyBpdCBmaXRzLgoKCmBgYHtyIGNjZGYsIGV2YWwgPSBUUlVFfQoKI2RmJG5ldHNpemUgPC0gcm91bmQocm93U3VtcyhkZlssYygxNDoxODUpXSkgLyBsZW5ndGgoMTQ6MTg1KSwgMCkKZGYgPC0gZGZbIWRmJG5ldHNvdmVyNiA+IDI1MDAsIF0KZGVncmVlcyA8LSByb3VuZChkZiRuZXRzb3ZlcjYsIDApCgpkZWdyX3BsIDwtIGRpc3BsJG5ldyhkZWdyZWVzKSAjIGNyZWF0ZSBhIGRpc2NyZXRlIHBvd2VybGF3IGRpc3RyaWJ1dGlvbiBvYmplY3QgCgojIHdpdGggZXN0aW1hdGluZyBsb3dlciB0aHJlc2hvbGQ6CmRlZ3JfbG5feG1pbiA8LSBkaXNsbm9ybSRuZXcoZGVncmVlcykKZXN0ID0gZXN0aW1hdGVfeG1pbihkZWdyX2xuX3htaW4pCmRlZ3JfbG5feG1pbiRzZXRYbWluKGVzdCkKCiMgd2l0aG91dCBsb3dlciB0aHJlc2hvbGQ6CmRlZ3JfbG5fbm94bWluIDwtZml0ZGlzdChkZWdyZWVzLCAibG5vcm0iKQoKIyBHb29kbmVzcyBvZiBmaXQgZm9yIGxvZ25vcm0sIG5vIHhtaW46CmdvZl9kZWdyX2xuX25veG1pbiA8LSBnb2ZzdGF0KGRlZ3JfbG5fbm94bWluLCBmaXRuYW1lcyA9ICJMb2ctbm9ybWFsIiwgZGlzY3JldGUgPSBUUlVFKQpnb2ZfZGVncl9sbl9ub3htaW4KCnhfc2VxIDwtIHNlcSgwLCBtYXgoZGVncmVlcyksIGxlbmd0aCA9IDUwMCkKCiMgRm9yIHBsb3R0aW5nIHRoZSBubyB4X21pbiB2ZXJzaW9uIG9mIExOCmxuX2ZpdF9jY2RmIDwtIDEgLSBwbG5vcm0oeF9zZXEsIG1lYW5sb2cgPSBkZWdyX2xuX25veG1pbiRlc3RpbWF0ZVsxXSwgc2Rsb2cgPSAgZGVncl9sbl9ub3htaW4kZXN0aW1hdGVbMl0pCgojIGNhcHR1cmUgZGF0YSB0aGF0IG1ha2UgdGhlIHBsb3QKcGQxIDwtIHBsb3QoZGVncl9wbCwgZHJhdyA9IEYpICMgcGxvdCBkYXRhIDEsIGVtcGlyaWNhbCBkaXN0cgpwZDIgPC0gbGluZXMoZGVncl9sbl94bWluLCBkcmF3ID0gRikgIyBwbG90IGRhdGEgMiBubyB4bWluCnBkMyA8LSBkYXRhLmZyYW1lKGNiaW5kKHhfc2VxLCBsbl9maXRfY2NkZikpICMgcGxvdCBkYXRhIDMgd2l0aCB4bWluCgojIG5vdyByZW5kZXIgaXQgYSBnZ3Bsb3QKY2NkZnBsb3QgPC0gZ2dwbG90KCkgKyAKICAgICAgICAgICAgICBnZW9tX3BvaW50KGRhdGE9cGQxLCBhZXMoeCA9IHgsIHkgPSB5KSwgc2hhcGU9MSkgKyAKICAgICAgICAgICAgICAjZ2VvbV9saW5lKGRhdGE9cGQyLCBhZXMoeCA9IHgsIHkgPSB5LCBjb2xvciA9ICJMb2ctbm9ybWFsIGZpdCwgdy8geF9taW4iKSkgKwogICAgICAgICAgICAgIGdlb21fbGluZShkYXRhPXBkMywgYWVzKHggPSB4X3NlcSwgeSA9IGxuX2ZpdF9jY2RmLCBjb2xvciA9ICJMb2ctbm9ybWFsIGZpdCwgbm8geF9taW4iKSkgKwogICAgICAgICAgICAgIGxhYnMoeD0iRXh0ZW5kZWQgbmV0d29yayBzaXplIiwgeT0iQ0NERiIpICsgCiAgICAgICAgICAgICAgc2NhbGVfY29sb3JfbWFudWFsKG5hbWUgPSAiRml0IiwgdmFsdWVzID0gYygjIkxvZy1ub3JtYWwgZml0LCB3LyB4X21pbiIgPSAiZ3JlZW4iLCAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICJMb2ctbm9ybWFsIGZpdCwgbm8geF9taW4iID0gInB1cnBsZSIpKSArCiAgICAgICAgICAgICAgdGhlbWVfYncoKSArCiAgICAgICAgICAgICAgdGhlbWUobGVnZW5kLnBvc2l0aW9uID0gYygwLjIyLCAwLjIpKSArCiAgICAgICAgICAgICAgc2NhbGVfeF9sb2cxMChicmVha3MgPSBjKDUwLDEwMCwyMDAsNTAwLDEwMDAsMjAwMCksIGxpbWl0cyA9IGMobWluKHBkMSR4KSwgbWF4KHBkMSR4KSkpICsgc2NhbGVfeV9sb2cxMCgpICsKICAgICAgICAgICAgICBnZ3RpdGxlKCJDQ0RGIHBsb3Qgb2YgYXZlcmFnZSBkZWdyZWUiKQoKIyBzYXZlCmdnc2F2ZSgib3V0cHV0L2NjZGZwbG90LnBkZiIsIHBsb3QgPSBjY2RmcGxvdCwgZGV2aWNlID0gInBkZiIsCiAgICAgICBzY2FsZSA9IDEsIHdpZHRoID0gNiwgaGVpZ2h0ID0gNCwgdW5pdHMgPSBjKCJpbiIpLAogICAgICAgZHBpID0gInJldGluYSIpCmdnc2F2ZSgib3V0cHV0L2NjZGZwbG90LmpwZWciLCBwbG90ID0gY2NkZnBsb3QsIGRldmljZSA9ICJqcGVnIiwKICAgICAgIHNjYWxlID0gMSwgd2lkdGggPSA2LCBoZWlnaHQgPSA0LCB1bml0cyA9IGMoImluIiksCiAgICAgICBkcGkgPSAicmV0aW5hIikKCiMgdHJ5b3V0IDwtIHBsb3RfZ3JpZChkZW5zMiwgZGVuczEsIGNjZGZwbG90LCBucm93ID0gMSkKIyAKIyBnZ3NhdmUoIm91dHB1dC9jb21wc19jb21iaW5lZC5wZGYiLCBwbG90ID0gdHJ5b3V0LCBkZXZpY2UgPSAicGRmIiwKIyAgICAgICAgc2NhbGUgPSAxLCB3aWR0aCA9IDE2LCBoZWlnaHQgPSA1LCB1bml0cyA9IGMoImluIiksCiMgICAgICAgIGRwaSA9ICJyZXRpbmEiKQoKIyMjIG9yaWdpbmFsIHBsb3QgaW4gQmFzZSByCiMgIyBQbG90dGluZyB0d28gdmVyc2lvbnMgb2YgTE4KIyBwbG90KGRlZ3JfcGwsIHhsYWI9Ik51bWJlciBvZiBjb250YWN0cyIsIHlsYWI9IkNDREYiKQojIGxpbmVzKGRlZ3JfbG5feG1pbiwgY29sID0gImdyZWVuIiwgbHdkID0gMikKIyBsaW5lcyh4X3NlcSwgbG5fZml0X2NjZGYsIGNvbCA9ICJwdXJwbGUiLCBsd2QgPSAyKQojIGxlZ2VuZCh4ID0gImJvdHRvbWxlZnQiLAojICAgICAgICBsZWdlbmQgPSBjKCJMb2ctbm9ybWFsIGZpdCwgdy8geF9taW4iLAojICAgICAgICAgICAgICAgICAgICJMb2ctbm9ybWFsIGZpdCwgbm8geF9taW4iIAojICAgICAgICAgICAgICAgICAgICksCiMgICAgICAgIGNvbCA9IGMoImdyZWVuIiwicHVycGxlIiksCiMgICAgICAgIGx3ZCA9IDIpCmNjZGZwbG90CmBgYAoKCgpgYGB7ciBwb3B2c2F2ZSwgZXZhbCA9IFRSVUV9CgpkZmFucyA8LSBkZlssIGMoInVuaSIsICJoYm8iLCAibWJvIiwgImRvY2h0ZXJ6b29uIiwgInR3ZWVsaW5nIiwgImNvcm9uYSIsIAogICAgICAgICAgICAgICJlbGF1dG8iLCAic2Nvb3RlciIsICJ2ZWdhbiIsIAogICAgICAgICAgICAgICJTb3BoaWUiLCAiSnVsaWEiLCJTYW5uZSIsIkxpc2EiLCJMYXVyYSIsIk1hcmlhIiwiTGluZGEiLCJKb2hhbm5hIiwiTW9uaXF1ZSIsIkVzdGVyIiwKICAgICAgICAgICAgICAiQW5uYSIsIkVsaXNhYmV0aCIsIkNvcm5lbGlhIiwiV2lsaGVsbWluYSIsIkFtaXJhIiwiU2FtaXJhIiwiU2FyYSIsIkRhYW4iLCJTZW0iLAogICAgICAgICAgICAgICJUaG9tYXMiLCJNYXgiLCJLZXZpbiIsIkpvaGFubmVzIiwiRGVubmlzIiwiSmVyb2VuIiwiSmFuIiwiTWFyY2VsIiwiQ29ybmVsaXMiLCJIZW5kcmlrIiwiUGV0cnVzIiwKICAgICAgICAgICAgICAiV2lsbGVtIiwiQWxpIiwiTW9oYW1tZWQiLCJOb29yIildICMgdGFrZSBtZWFuIG9mIGVhY2ggb2YgdGhlIGNhdHMKbWVhbnMgPC0gY29sTWVhbnMoZGZhbnMpCgoKCgoKcmVmMSA8LSBjKDg0OTU3LCA3NTIxNCwgMTQ1NjAwLCAxNjgwNjYsIDI1MDAsIDE1NTg1NDkpCiMgT1JERVI6ICB1bmksIGhibywgbWJvLCBkb2NodGVyL3pvb24sIHR3ZWVsaW5nLCBjb3JvbmEKCgpyZWYyIDwtIGMoMjczMjU5LCA0NjA2MTgsIDI2MTAwMCkKIyBPUkRFUjogICBlbGVjYXV0bywgc2Nvb3RlciwgdmVnYW4sCgpyZWYzIDwtIGMoMTUyNzYsMTYzNTAsMjczOTQsMjEyMDAsMjU2ODEsMzM0NTAyLDI5OTU1LDI2NjUyMiwzOTQ4MSwgMjY5MiwKICAgICAgICAgIDEzNjI5NiwxMTAyMzEsMTEyODA3LDk4MjA4LDEzODYsMjE4NiwxMTY0MCwyMjcwNCwxMzI3NiwKICAgICAgICAgIDQwNTQzLDE3MDI0LDIzMTY3LDMwNzAzMiwzNjQxMSw0OTE4MiwxODY3NDYsMzU5NzMsMTM0OTU2LDExODYxMCw4NjUwMCwKICAgICAgICAgIDEwMjI5Niw0MjEzLDUwMDMsNDUxNykKIyBPUkRFUjogICBTb3BoaWUsIEp1bGlhLFNhbm5lLExpc2EsTGF1cmEsTWFyaWEsTGluZGEsSm9oYW5uYSxNb25pcXVlLEVzdGVyLAojICAgICAgICAgICAgIEFubmEsRWxpc2FiZXRoLENvcm5lbGlhLFdpbGhlbG1pbmEsQW1pcmEsU2FtaXJhLFNhcmEsRGFhbixTZW0sCiMgICAgICAgICAgICAgVGhvbWFzLE1heCxLZXZpbixKb2hhbm5lcyxEZW5uaXMsSmVyb2VuLEphbixNYXJjZWwsQ29ybmVsaXMsSGVuZHJpayxQZXRydXMsCiMgICAgICAgICAgICAgV2lsbGVtLEFsaSxNb2hhbW1lZCxOb29yCgpwb3BzIDwtIGMocmVmMSwgcmVmMiwgcmVmMykKCmZpZyA8LSBkYXRhLmZyYW1lKGNiaW5kKG1lYW5zLCBwb3BzKSkKCgoKY29yKGZpZ1shZmlnJHBvcHMgPiA1MDAwMDAsIF0pCmNvcihmaWdbIWZpZyRwb3BzID4gMjAwMDAwLCBdKQpjb3IoZmlnW2ZpZyRwb3BzIDwgNTAwMDAsIF0pCmNvcihmaWdbZmlnJHBvcHMgPCAxMDAwMDAsIF0pCgoKZXgzIDwtIGdncGxvdChmaWcsIGFlcyh4PXBvcHMsIHk9bWVhbnMpKSArIAogIGdlb21fcG9pbnQoKSArIAogIHhsaW0oeD0gYygwLCA1MDAwMCkpICsgCiAgeWxpbShjKDAsMi41KSkgKyAKICBnZW9tX3Ntb290aChtZXRob2Q9J2xtJykgKwogIGdlb21fdGV4dChsYWJlbCA9IHJvd25hbWVzKGZpZyksCiAgICAgICAgICAgIG51ZGdlX3kgPSAwLjEpICsKICB0aGVtZV9taW5pbWFsKCkgKwogIHhsYWIoIlBvcHVsYXRpb24gc2l6ZSIpICsKICB5bGFiKCJBdmVyYWdlIG51bWJlciBtZW50aW9uZWQiKSArCiAgc21fc3RhdENvcnIoKSArIAogIGdndGl0bGUoIkMpIFBvcHVsYXRpb24gc2l6ZSA8NTBrIikKZXgzCgpleDIgPC0gZ2dwbG90KGZpZywgYWVzKHg9cG9wcywgeT1tZWFucykpICsgCiAgZ2VvbV9wb2ludCgpICsgCiAgeGxpbSh4PSBjKDAsIDUwMDAwMCkpICsgCiAgeWxpbShjKDAsMi41KSkgKyAKICBnZW9tX3Ntb290aChtZXRob2Q9J2xtJykgKwogIGdlb21fdGV4dChsYWJlbCA9IHJvd25hbWVzKGZpZyksCiAgICAgICAgICAgIG51ZGdlX3kgPSAwLjEpICsKICB0aGVtZV9taW5pbWFsKCkgKwogIHhsYWIoIlBvcHVsYXRpb24gc2l6ZSIpICsKICB5bGFiKCJBdmVyYWdlIG51bWJlciBtZW50aW9uZWQiKSArCiAgc21fc3RhdENvcnIoKSsgCiAgZ2d0aXRsZSgiQikgUG9wdWxhdGlvbiBzaXplIDw1MDBrIikKZXgyCgpleDEgPC0gZ2dwbG90KGZpZywgYWVzKHg9cG9wcywgeT1tZWFucykpICsgCiAgZ2VvbV9wb2ludCgpICsgCiAgZ2VvbV9zbW9vdGgobWV0aG9kPSdsbScpICsKICBnZW9tX3RleHQobGFiZWwgPSByb3duYW1lcyhmaWcpLAogICAgICAgICAgICBudWRnZV95ID0gMC4xKSArCiAgdGhlbWVfbWluaW1hbCgpICsKICB4bGFiKCJQb3B1bGF0aW9uIHNpemUiKSArCiAgeWxhYigiQXZlcmFnZSBudW1iZXIgbWVudGlvbmVkIikgKwogIHNtX3N0YXRDb3JyKCkgKyAKICBnZ3RpdGxlKCJBKSBBbGwgcG9wdWxhdGlvbiBzaXplcyIpCmV4MQoKZXggPC0gY293cGxvdDo6cGxvdF9ncmlkKGV4MSwgZXgyLCBleDMsIG5yb3cgPSAxKQoKZ2dzYXZlKCJvdXRwdXQvcG9wc2l6ZXMucGRmIiwgcGxvdCA9IGV4LCBkZXZpY2UgPSAicGRmIiwKICAgICAgIHNjYWxlID0gMSwgd2lkdGggPSAxNiwgaGVpZ2h0ID0gNSwgdW5pdHMgPSBjKCJpbiIpLAogICAgICAgZHBpID0gInJldGluYSIpCmdnc2F2ZSgib3V0cHV0L3BvcHNpemVzLmpwZWciLCBwbG90ID0gZXgsIGRldmljZSA9ICJqcGVnIiwKICAgICAgIHNjYWxlID0gMSwgd2lkdGggPSAxNiwgaGVpZ2h0ID0gNSwgdW5pdHMgPSBjKCJpbiIpLAogICAgICAgZHBpID0gInJldGluYSIpCmV4CmBgYAoKCgoKCgo=